控制系统实践4 - 非线性控制

前面我们讨论的所有系统均为线性系统，线性系统的分析和设计方法已经相当成熟和完善。但实际物理世界中的完美线性系统几乎不存在，摩擦、迟滞、饱和等各种非线性特性是几乎无法避免的，也因此发展出了一套非线性系统的分析和控制的方法。本小节简单介绍非线性控制中的反馈线性化、自适应控制和滑模控制等方法。

考虑在电机输出轴安装一个悬臂负载，则系统的动力学模型如下：

$$K_m\dot w(t)+K_fw(t)=K_ii_a(t)+K_g \sin(\theta)$$

可以看出此时系统存在一个非线性项$K_g\sin(\theta)$。此时若采用前面设计的PI控制器进行速度控制，则系统会由于非线性项的影响而存在周期性的波动：

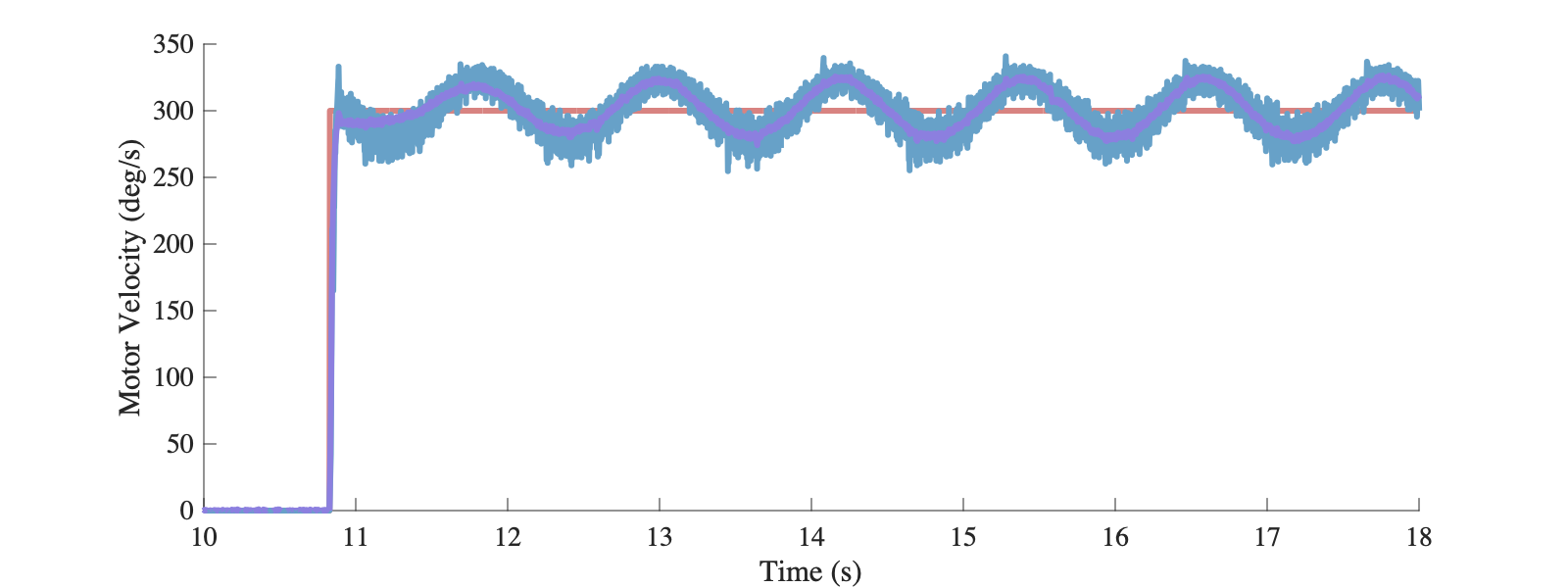
反馈线性化

$$K_m\dot w(t)+K_fw(t)=K_ii_a(t)+K_g \sin\theta$$

对于结构明确、参数已知的非线性系统，一个很自然的想法就是通过适当的变换，将系统非线性部分消除掉，再对变换后的线性系统采用经典控制或现代控制的方法设计控制器。例如考虑构建新的控制量$i_u$：

$$i_u=i_a+\frac{K_g}{K_i}\sin\theta$$

则变换后系统的模型为：

$$K_m\dot w(t)+K_fw(t)=K_ii_u(t)$$

根据前面的分析，对于变换后的线性系统我们设计PI控制器：

$$i_u=K_p(w_{d}-w)+K_i\int(w_{d}-w)dt$$

则总的电机控制电流为：

$$i_a=K_p(w_{d}-w)+K_i\int(w_{d}-w)dt-\frac{K_g}{K_i}\sin\theta$$

这里我们实现最简单的反馈线性化形式，对于更复杂的非线性系统有着更系统的反馈线性化理论。

我们实际上是通过驱动电流补偿负载转矩，来消除系统的非线性项，从而修改了系统模型。前面我们介绍过测速反馈也是一种修改模型的方法，和这里的反馈线性化是相似的思想。实际上仅通过上面的反馈线性化部分，就可以实现负载的重力补偿：

$$i_a=-\frac{K_g}{K_i}\sin\theta$$

自适应控制

在上面的反馈线性化中，系统的非线性结构和参数是完全已知。但在实际系统中，我们可能无法预先知道参数的大小，甚至是非线性的结构。对非线性结构已知、参数未知的情况，可以通过辨识非线性参数，进而通过反馈线性化实现稳定控制，由此发展了模型参考自适应控制和自校正控制，这里我们 介绍前一种方法。

考虑动力学模型：

$$\dot w(t)+K_fw(t)=K_ii_a(t)+K_g \sin(\theta)$$

其中$K_g$为恒定或缓慢变化的未知参数，为简化后面的表达，所有参数对$K_m$归一化。

由于$K_g$未知，因此对构造一个估计变量$\hat K_g$，估计误差为：

$$\tilde K_g=K_g-\hat K_g$$ $$\dot{\tilde K_g}=\dot K_g-\dot{\hat K_g}=-\dot{\hat K_g}$$

考虑对于期望转速$w_d$的跟踪问题，跟踪误差为：

$$e=w_d-w$$ $$\dot e = \dot w_d-\dot w=\dot w_d-(-K_fw+K_ii_a+K_g\sin\theta)$$

设计如下控制器和参数估计器：

$$i_a=\frac{1}{K_i}(\dot w_d+K_fw-\hat K_g\sin\theta+ke)$$ $$\dot{\hat K_g}=-\gamma e \sin\theta$$

则有：

$$\begin{align} \dot e &=\dot w_d-[-K_fw+(\dot w_d+K_fw-\hat K_g\sin\theta+ke)+K_g\sin\theta]\\ &=-ke-(K_g-\hat K_g)\sin\theta\\ &=-ke-\tilde K_g\sin\theta \end{align}$$

构造李雅普诺夫函数：

$$\begin{align} V&=\frac{1}{2}e^2+\frac{1}{2\gamma}{\tilde K_g}^2\\ \dot V&=e\dot e+\frac{1}{\gamma}{\tilde K_g}\dot{\tilde K_g}\\ &=e(-ke-\tilde K_g\sin\theta)-\frac{1}{\gamma}{\tilde K_g}\dot{\hat K_g}\\ &=-ke^2-\tilde K_ge\sin\theta +\tilde K_ge\sin\theta\\ &=-ke^2 \end{align}$$

因此自适应系统是全局稳定的，Barbalat引理保证跟踪误差全局渐进收敛。

在具体实现代码实现时，阶跃曲线的$\dot w_d=0$，$i_a=\frac{1}{K_i}(K_fw-\hat K_g\sin\theta+ke)$，其中$(K_fw-\hat K_g\sin\theta)$是通过估计参数进行反馈线性化，$ke$是比例控制。我们也可以根据设计成其他形式的自适应控制器，例如采取比例积分方法：

$$\begin{align*} i_a&=K_pe+K_i\int e dt-\hat K_g^{'}\sin\theta\\ \dot{\hat K_g^{'}}&=-\gamma e \sin\theta \end{align*}$$

其中$K_g^{‘}=\frac{K_g}{K_i}$。dSAPCE的代码如下：

e = des_vel - motor_vel;
e_i = e_i + e*Ts;
theta = 2*pi*motor_pos/180;
Kg = Kg - gamma*e*sin(theta)*Ts;
ia = Kp*e + Ki*e_init + Kg*sin(theta);

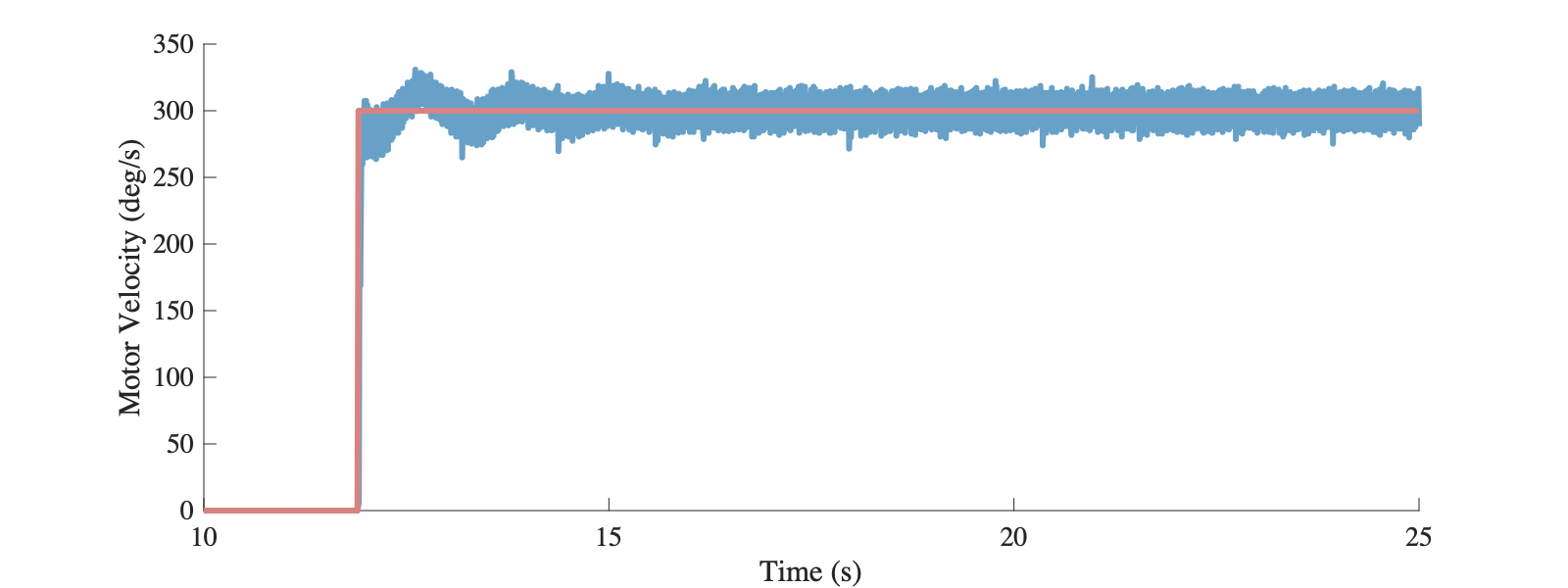
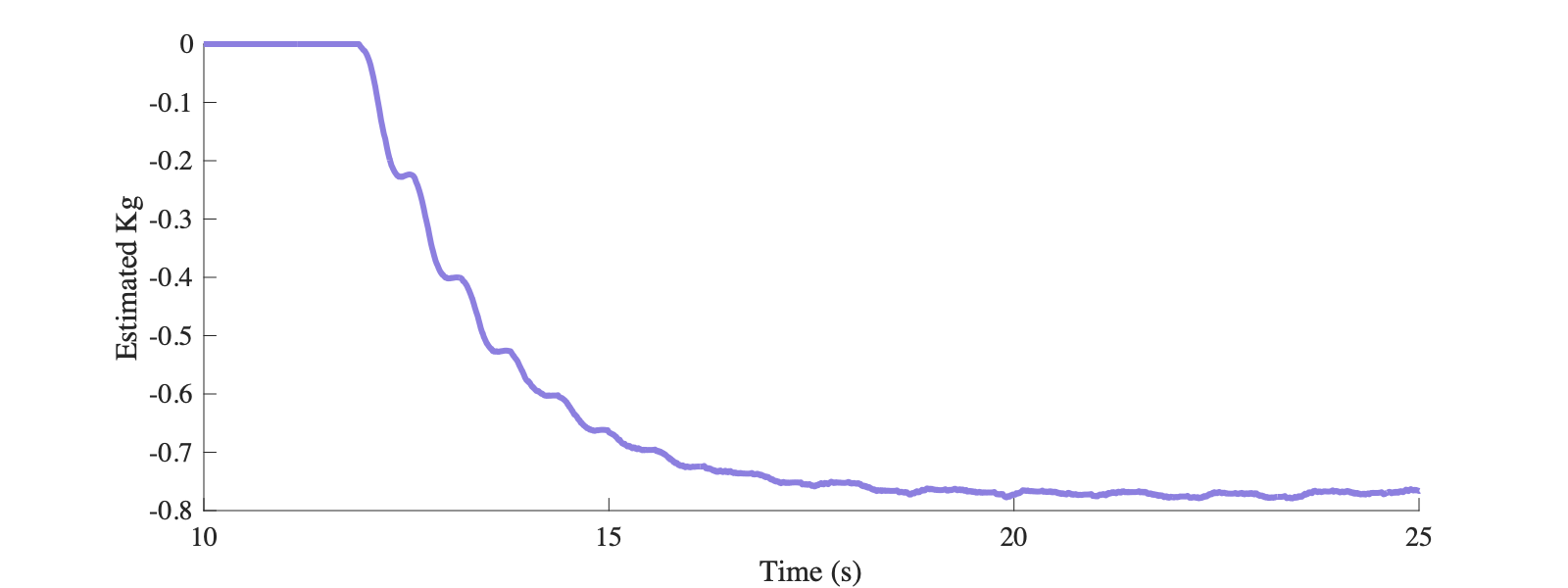
从实验结果可以看出，随着自适应学习过程的推进，参数估计逐渐准确，非线性的影响逐渐被抵消。

滑模控制

滑模控制是另一种处理非线性系统模型不确定的方法，它考虑系统的参数快速变化、或是模型结构未知的情况，但所有的不确定项存在一个上确界函数。例如：

$$\dot w(t)+K_fw(t)=K_ii_a(t)+f(w)$$ $$|f(x)|<\rho(w)=(K_g+\epsilon)|sin(\theta)|$$

同样考虑跟踪期望转速$w_d$问题，跟踪误差为：

$$\begin{align*} e&=w_d-w\\ \dot e &= \dot w_d-\dot w=\dot w_d-(-K_fw+K_ii_a+f(w)) \end{align*}$$

设计控制器：

$$i_a=\frac{1}{K_i}[\dot w_d+K_fw+ke+\rho\cdot sgn(e)]$$

则有：

$$\dot e =-ke - f - \rho\cdot sgn(e)$$

构造李雅普诺夫函数：

$$\begin{align*} V&=\frac{1}{2}e^2\\ \dot V&=e\dot e\\ &=e[-ke-f- \rho\cdot sgn(e)]\\ &=-ke^2-fe-\rho|e|\\ &\le -ke^2 + |f||e|-\rho|e|\\ &\le -ke^2 + \rho|e|-\rho|e|\\ &=-ke^2 \end{align*}$$

由Lyapunov-like Lemma可知系统全局渐进稳定。通过一下代码在dSPACE中实现滑模控制

e = des_vel - motor_vel;
theta = 2*pi*motor_pos/180;
rho = Kr*abs(sin(theta))
ia = Kp*e + Ki*e_init + rho*sign(e);

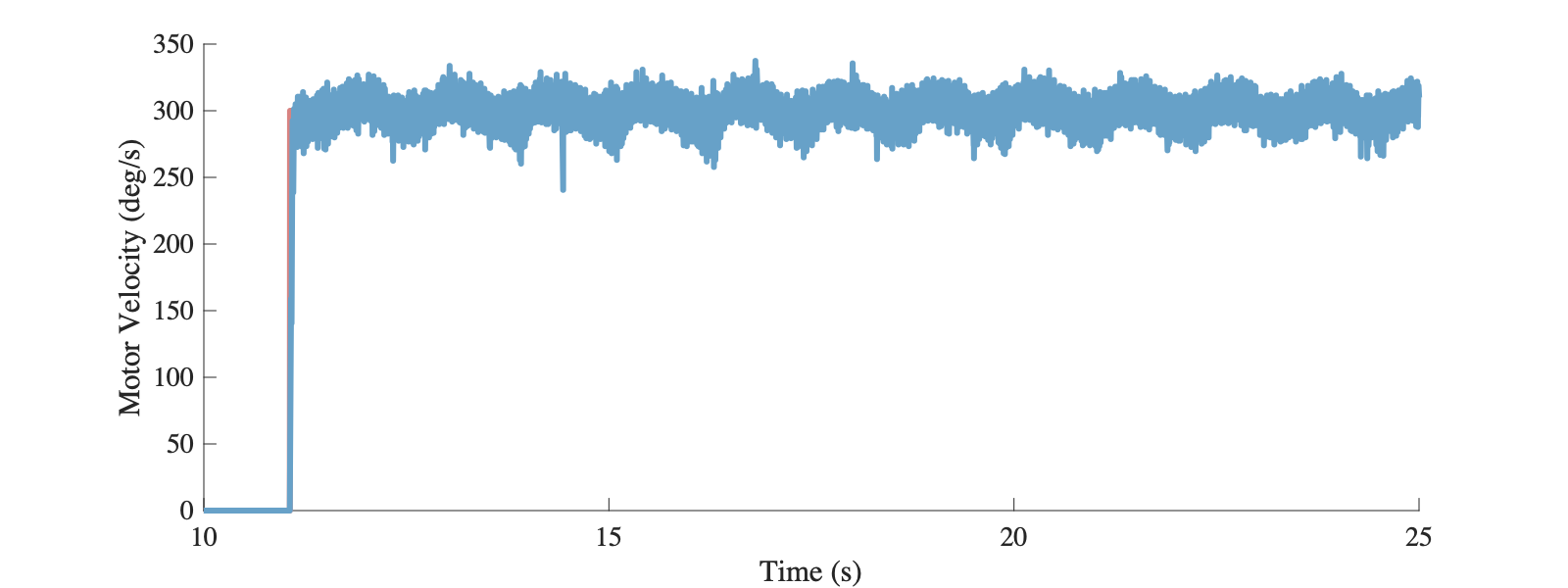
在具体实现时，滑模控制是通过产生较大的控制输出来将系统强行到期望“滑模面”上，并容易出现抖振现象，电机电流波动震荡较大。